Introduction

The digital transformation of commerce has established online platforms as central arenas for retail activity, profoundly shaping how consumers discover and purchase goods. Amidst marketplace giants, a diverse ecosystem of platforms (including Shopify, WooCommerce, Adobe Commerce, BigCommerce, and PrestaShop) empowers millions of merchants globally. These platforms provide essential sales infrastructure, but in the highly competitive online environment, effective Digital Merchandising—the strategic presentation and organization of products—is paramount for capturing attention and driving conversion.

A critical aspect of digital merchandising is determining the order in which products appear on category and search pages. Two primary paradigms govern this: traditional Fixed Global Sorting, where merchants impose a consistent order (e.g., manual ‘featured’ placement, ‘best-selling’, price) across broad user segments, and Hyper-Personalized Recommendations. Driven by significant recent advances in AI and data analytics, hyper-personalization aims to dynamically tailor product rankings to individual user preferences, promising enhanced relevance.

While fixed global sorting offers merchants predictability and control—often facilitated through platform tools for manual arrangement or rule-based ordering—this ‘one-size-fits-all’ approach may not optimally cater to diverse consumer needs. Its effectiveness is primarily understood through established behavioral principles, framed by the concept of Choice Architecture. The design of the storefront intrinsically shapes user decisions. Global sorting heavily leverages the primacy effect, granting disproportionate visibility to top-listed items, but can also inadvertently exacerbate choice overload or misrepresent catalogue diversity if not carefully implemented. Furthermore, the default sort order acts as a powerful nudge within this choice architecture, significantly influencing user navigation and perception.

Evaluating the true impact of emerging hyper-personalization against these established global sorting techniques poses considerable challenges, particularly in simulating the complexity of personalization algorithms. These engines frequently represent users ($u$) and products ($x_i$) as embeddings in a finite-dimensional space $\mathbb{R}^k$, ranking items based on metrics like the dot product $u^T x_i$. Understanding the potential diversity of rankings generated by such systems is crucial. Concepts from statistical learning theory, particularly related to Vapnik-Chervonenkis (VC) theory and hyperplane arrangements, provide insight into the expressive capacity of these linear preference models. For $n$ products in $\mathbb{R}^k$ (assuming general position), the maximum number of distinct rankings inducible by varying the user preference vector $u$ is theoretically bounded by $N = 2\sum_{i=0}^{k-1} \binom{n-1}{i}$. This number $N$ grows astronomically with typical e-commerce catalogue sizes ($n$) and embedding dimensions ($k$).

If we assume that for a diverse catalogue and user base, the embedding process yields user and product vectors approximating a reasonably uniform or random distribution within $\mathbb{R}^k$, then the vast range of possible user preferences will likely generate a correspondingly vast array of distinct personalized rankings across the population. This sheer variability implies that, from an aggregate viewpoint, the presentation order might appear highly varied or ‘pseudo-random’.

This paper investigates the emergent sales outcomes resulting from distinct sorting strategies: Fixed Global Sorting versus Hyper-personalization. Our unique contribution analyzes these through the lenses of Choice Architecture and Digital Merchandising. Critically, we diverge from standard recommendation systems literature, which typically assumes personalization boosts engagement metrics like click-through rates (CTR). Instead, we hold interaction probabilities constant, isolating the impact of the sorting architecture on sales performance. Using a simulation model, we show that, under certain conditions, the hyper-personalized approach can yield superior sales outcomes compared to fixed global sorting, demonstrating the potential of hyper-personalization to enhance sales performance inside an increasingly competitive landscape.

This paper proceeds by outlining the simulation methodology, detailing the model’s structure, parameters, and the implementation of the two experimental conditions. We then present the simulation results, analyze the observed differences, and discuss the implications for Digital Merchandising strategy, considering the trade-offs between controlled global merchandising and the potential reflected by our personalization proxy, before suggesting directions for future research.

Methodology

Simulation Framework

In the domain of e-Commerce, a digital catalogue serves as the primary interface for customers to browse available items. This catalogue, denoted by $\mathcal{C}$, is composed of a set of products. Let the total number of distinct products be $N_p$. Each product $P_i$ (for $i=1, \dots, N_p$) represents a unique item offered for sale.

Products are organized within a predefined category hierarchy structure to aid discovery. This hierarchy consists of $L$ levels. For each level $k \in \{1, \dots, L\}$, there are $L_k$ distinct categories. Each product $P_i$ is assigned to a specific category at each level of this hierarchy. This assignment is represented by a sequence $C_i = (c_{i,1}, c_{i,2}, \dots, c_{i,L})$, where $c_{i,k}$ is the identifier of the category assigned to product $P_i$ at level $k$. Typically, these identifiers are integers such that $c_{i,k} \in \{1, 2, \dots, L_k\}$. This sequence $C_i$ defines the product’s unique path through the hierarchy- with $c_{i,1}$ representing “Electronics,” $c_{i,2}$ representing “Laptops”, and $c_{i,3}$ representing “Gaming Laptops”.

Products $P_i$ can also exist in multiple variations, known as variants, which distinguish attributes like size, color, or configuration. Let $V_i$ denote the set of variants for product $P_i$. Each specific variant $v_{i,j} \in V_i$ (where $j=1, \dots, |V_i|$) has an associated stock quantity, $q(v_{i,j}) \ge 0$, representing the number of units currently available. Thus, $V_i$ captures the specific purchasable forms of product $P_i$ and their availability.

Catalogue Generation

The generation of the synthetic catalogue $\mathcal{C}$ involves specifying the properties for each of the $N_p$ products. For a single product $P_i$, this involves determining its category assignment sequence, $C_i$, and its set of variants, $V_i$, along with their initial stock levels. The process follows these steps of Hierarchy Assignment and Variant Generation, which are detailed below.

Product Hierarchy Assignment

Given the predefined category hierarchy structure with $L$ levels and $L_k$ distinct categories available at each level $k \in \{1, \dots, L\}$, we generate the category assignment sequence for product $P_i$, denoted $C_i = (c_{i,1}, c_{i,2}, \dots, c_{i,L})$. Each element $c_{i,k}$ (the category ID at level $k$) is determined by independently sampling from the available categories at that level:

This process assigns product $P_i$ to a randomly selected complete path through the category structure.

Product Variant Generation

Generating the variants for product $P_i$ involves determining their number and initial stock quantities.

The number of distinct variants for product $P_i$, denoted $|V_i|$, is sampled from a discrete uniform distribution, where $U_v$ is the maximum allowable number of variants per product:

For each of the $|V_i|$ variants, we first assign a unique identifier $v_{i,j}$ (for simplicity, we can let $v_{i,j}$ correspond to the index $j$, where $j=1, \dots, |V_i|$). The initial stock quantity for each variant, $q(v_{i,j})$, is then sampled independently from a Poisson distribution with rate parameter $\lambda_q$:

Conceptually, $V_i = \{ v_{i,1}, \dots, v_{i, |V_i|} \}$ is the set of variant identifiers for product $P_i$, and $q$ is a function mapping each $v_{i,j} \in V_i$ to its non-negative integer stock level. For practical representation, this information is often stored as a collection of pairs: $\{ (v_{i,j}, q(v_{i,j})) \mid j=1, \dots, |V_i| \}$.

User Query Simulation

User interactions with the catalogue are simulated as queries arriving sequentially. Each query represents a user session aimed at finding products within a specific context, potentially leading to a purchase. The simulation of a single user query involves defining the query context, identifying relevant products, presenting them according to a specified sorting logic, handling user interaction (purchase attempt), and updating the system state.

Query Context Specification

Each query is defined by the user’s navigation choices: the category they browse and the page number they view.

Users may navigate through the category hierarchy (defined by $L$ levels with $L_k$ categories at level $k$). The simulated user selects a category path $C_q = (c_{q,1}, c_{q,2}, \dots, c_{q,k_q})$, where $k_q \le L$ is the depth of the selected path. This path is determined probabilistically level by level: Starting at level $l=1$, with probability $\rho_h$, the user selects a specific category $c_{q,l}$ uniformly from the $L_l$ available categories at that level ($\text{Uniform}\{1, \dots, L_l\}$) and proceeds to level $l+1$. With probability $1-\rho_h$, the user stops refining the path at the current level, finalizing $C_q$ with length $k_q = l-1$. If the user stops at $l=1$, the path $C_q$ is empty ($k_q=0$), indicating no category filter is applied.

Users browse products page by page. The requested page number $p$ ($p \ge 1$) is sampled from a Geometric distribution with parameter $(1-\rho_p)$, where $\rho_p$ is the probability of navigating to the next page: $P(p=k) = \rho_p^{k-1} (1-\rho_p)$. This models diminishing likelihood of viewing subsequent pages.

The query context is thus defined by the pair $(C_q, p)$.

Product Filtering

Based on the selected category path $C_q$ (of length $k_q$), the system filters the main catalogue $\mathcal{C}$ to find matching products. A product $P_i$ with category assignment $C_i = (c_{i,1}, \dots, c_{i,L})$ matches if its first $k_q$ category assignments match the query path. The filtered set is:

Let $N_{filt} = |\mathcal{C}_{filtered}|$ be the number of products matching the query filter.

Pagination

The system determines the total number of products, $N_{ret}$, potentially viewable by the user up to the requested page $p$. This depends on the number of products displayed per page, $s$:

This $N_{ret}$ represents the size of the product pool from which the user’s view is constructed.

Product Presentation Logic (Sorting)

The core of Digital Merchandising lies in how products are ordered. We simulate two distinct sorting functions: the Global Fixed Sorting Function ($\text{SortGlobal}$) and the Hyper-Personalized Sorting Function ($\text{SortHyperPersonalized}$). These functions determine the order in which products are presented to the user after filtering.

The Global Fixed Sorting Function ($\text{SortGlobal}$) represents traditional merchandising where products are presented in a consistent, predefined order across all users (e.g., sorted by sales rank, price, or manual curation). Given the filtered set $\mathcal{C}_{filtered}$ and the target count $N_{ret}$, this function returns the first $N_{ret}$ products according to that global order.

where $P_{(j)}$ is the $j$-th product in the global order within $\mathcal{C}_{filtered}$.

The Hyper-Personalized Sorting Function ($\text{SortHyperPersonalized}$) aims to capture the essence of modern recommendation systems that tailor rankings to individual users. Such systems often embed users ($u$) and products ($x_i$) into a vector space $\mathbb{R}^k$ and rank items based on similarity (e.g., $u^T x_i$). As discussed in the introduction, VC theory suggests that even simple linear models can generate an large number of distinct rankings ($N = 2\sum_{i=0}^{k-1} \binom{n-1}{i}$ for $n$ products in $\mathbb{R}^k$). If user preferences ($u$) and product attributes ($x_i$) are sufficiently diverse across the population and catalogue, the resulting personalized rankings for different users will vary significantly. Simulating individual user vectors ($u$) and optimizing rankings for each query is computationally intensive. Given the theoretical potential for extreme variability in rankings across users, we use a pseudo-random presentation as a computationally tractable proxy for the aggregate effect of hyper-personalization, by selecting $N_{ret}$ products uniformly at random without replacement from the filtered set $\mathcal{C}_{filtered}$.

User Interaction and Purchase Attempt

Once products $\mathcal{P}_{disp}$ are presented, we simulate potential user actions. To simulate an action we assume the user has an implicit preference for a specific variant characteristic, represented by a preferred variant ID $v_p$, as in the product listing the user is presented with the Product and not a Variant, the specific Variants and their availability to the user is only known to the User after clicking on the product. This Variant preference is sampled uniformly from the set of all possible product variants using:

For a product $P_i \in \mathcal{P}_{disp}$ potentially considered by the user a purchase takes place if the following conditions are met:

1. A click occurs (with probability $P(\text{click})$),
2. If clicked, the user has purchase intent (with probability $P(\text{intent})$),
3. The preferred variant $v_p$ is offered for product $P_i$, and
4. There is available stock, denoted $q(v_{i, j^*}) > 0$, for the preferred variant $v_{i, j^*}$.

When a successful purchase of product $P_i$ occurs via its specific variant $v_{i, j^*}$ (corresponding to the user’s preferred variant ID $v_p$), the system state is updated immediately to reflect the transaction and manage availability:

• Decrement Stock: The available stock for the purchased variant is reduced by one:
  $$q(v_{i, j^*}) \leftarrow q(v_{i, j^*}) - 1$$
• Variant Availability Update: If the stock $q(v_{i, j^*})$ reaches zero due to this purchase, this specific variant $v_{i, j^*}$ becomes unavailable and cannot satisfy future purchase attempts requiring it.
• Product Availability Update: After the variant stock is updated, the system checks if all variants of product $P_i$ now have zero stock. If all variants are out of stock, the entire product $P_i$ is marked as unavailable and removed from the catalogue. This ensures that the product is no longer presented in future queries.

Analytical Expectations and Factors Influencing Sorting Divergence

In this section, we analyze conditions under which the hyper-personalized sorting function produces meaningfully different product rankings compared to fixed global sorting. Specifically, we examine the expected sizes of the filtered product set $\mathcal{C}_{filtered}$ and the displayed product set $\mathcal{P}_{disp}$ to characterize scenarios where:

We first establish the expected size of the filtered catalogue, $\mathbb{E}[|\mathcal{C}_{filtered}|]$. Given the catalogue size $|\mathcal{C}|$ and the probabilistic nature of user navigation through the hierarchical category structure, we start by considering the number of possible category-based partitions at various depths. The maximum number of leaf categories in a hierarchy with depth $L$ is defined as:

where $L_k$ is the number of distinct categories at hierarchy level $k$. However, because users probabilistically choose their stopping depth based on the parameter $\rho_h$, the expected number of effective leaf categories visited by users is given by:

Here, the term $\rho_h^{k-1}(1-\rho_h)$ represents the probability that users stop their navigation precisely at level $k$. The expected size of the filtered catalogue can thus be expressed as:

Next, we calculate the expected number of products displayed to users, $\mathbb{E}[|\mathcal{P}_{disp}|]$. Given users browse pages according to a geometric distribution with continuation probability $\rho_p$ and page size $s$, the expected number of viewed products across all pages is:

For meaningful differentiation between the sorting methods to emerge, the displayed product set must be strictly smaller than the available filtered set, providing room for variation in sorting outcomes. Therefore, a necessary condition for hyper-personalization to differ substantially from global sorting is:

This inequality implies that the number of products users view must be sufficiently limited relative to the filtered catalogue size, enabling personalized sorting to meaningfully vary product presentation between users. If this condition is not satisfied, the hyper-personalized sorting will closely resemble the global sorting, reducing personalization’s potential benefits. Understanding this constraint is critical when evaluating the strategic value of hyper-personalization within digital merchandising contexts.

Null Hypothesis

We investigate whether the choice of sorting strategy—Fixed Global Sorting versus Hyper-Personalized Sorting—significantly influences the cumulative number of purchases, denoted by $P(t)$, as a function of the number of user queries $t$.

Let:

• $P(t)$ be the cumulative number of purchases after $t$ queries.
• $\mu_{\text{G}}(t) = \mathbb{E}[P(t) \mid \text{Global Sorting}]$ be the expected cumulative purchases under the Fixed Global Sorting condition.
• $\mu_{\text{H}}(t) = \mathbb{E}[P(t) \mid \text{Hyper-Personalized Sorting}]$ be the expected cumulative purchases under the Hyper-Personalized Sorting condition.

The hypotheses are defined as follows:

• Null Hypothesis ($H_0$): The sorting strategy does not affect the cumulative purchases, meaning the expected purchase trajectories are identical for both conditions:
  $$H_0: \mu_{\text{G}}(t) = \mu_{\text{H}}(t) \quad \text{for all relevant } t.$$
  Under $H_0$, any observed differences in $P(t)$ are attributed solely to random variation.
• Alternative Hypothesis ($H_1$): There exists at least one query count $t$ for which the expected cumulative purchases differ between the two sorting strategies:
  $$H_1: \exists \, t \text{ such that } \mu_{\text{G}}(t) \neq \mu_{\text{H}}(t).$$

Statistical Approach: Bootstrapping Uplift

Due to the complex, path-dependent nature of our simulation outputs and the absence of an analytical distribution for cumulative purchases, we employ a non-parametric bootstrap approach. This method directly estimates uncertainty and constructs confidence intervals for the relative uplift in cumulative purchases between the two sorting strategies.

Let:

• $P_G^{(i)}(t)$ denote the cumulative number of purchases after $t$ queries for the $i$-th run under the Fixed Global Sorting condition.
• $P_H^{(i)}(t)$ denote the cumulative number of purchases after $t$ queries for the $i$-th run under the Hyper-Personalized Sorting condition.

Assume that $n$ independent simulation runs are available for each condition. The bootstrap procedure is as follows:

1. Resampling: Perform $B$ bootstrap iterations (e.g., $B = 10{,}000$). In each iteration $b$:

   • Draw, with replacement, a simulation run from the $n$ Global Sorting runs to obtain the trajectory $P_{G,b}(t)$.
   • Draw, with replacement, a simulation run from the $n$ Hyper-Personalized Sorting runs to obtain the trajectory $P_{H,b}(t)$.

2. Uplift Calculation: For each bootstrap sample $b$ and each query point $t$ where $P_{G,b}(t) > 0$, compute the relative uplift:

   $$U_b(t) = \frac{P_{H,b}(t) - P_{G,b}(t)}{P_{G,b}(t)}$$

   This produces $B$ bootstrap replicates of the uplift time series $U(t)$.

3. Empirical Distribution: The collection $\{ U_b(t) \}_{b=1}^{B}$ forms the empirical bootstrap distribution for the relative uplift at each query point $t$.

4. Confidence Interval Estimation: For each $t$, determine the 5th and 95th percentiles of the bootstrap distribution, denoted $p_{0.05}(U(t))$ and $p_{0.95}(U(t))$, respectively. These percentiles define a 90% confidence interval:

   $$\text{CI}_{90}(U(t)) = \left[ p_{0.05}(U(t)), \; p_{0.95}(U(t)) \right].$$

The confidence intervals for $U(t)$ are used to evaluate our null hypothesis $H_0$ at each query point $t$:

• If $\text{CI}_{90}(U(t))$ does not include zero, we reject $H_0$ at the $\alpha = 0.10$ significance level for that query point, indicating a statistically significant difference in cumulative purchases between the two sorting conditions.
• If $\text{CI}_{90}(U(t))$ includes zero, we fail to reject $H_0$, suggesting that the observed uplift is not statistically distinguishable from zero given the simulation variability.

Consistent rejection of $H_0$ over a relevant range of $t$ provides robust evidence that the sorting strategy exerts a persistent and statistically significant impact on purchase dynamics. Visualizing the mean relative uplift $\mathbb{E}[U(t)]$ along with its bootstrap confidence intervals over $t$ offers a clear graphical assessment of the magnitude, duration, and significance of the sorting effect.

Parameter Space

The simulation experiments were conducted using a fixed set of parameters that define the synthetic e-commerce environment, the characteristics of simulated user behavior, and the simulation duration. The catalogue consists of $N_p = 18000$ products, which are organized within a three-level hierarchy. At the first level, there are $L_1 = 30$ categories; and at the second level, each top-level category is subdivided into $L_2 = 7$ sub-categories. This structure yields a total of $30 \times 7 = 210$ distinct leaf categories. Each product is assigned a number of variants drawn from a discrete uniform distribution on $\{1, 2, 3, 4, 5\}$, with $U_v = 5$ representing the maximum possible variants per product. The initial stock level for each variant is determined by sampling from a Poisson distribution with mean $\lambda_q = 12.0$.

User behavior in the simulation is modeled through several probabilistic parameters. The paging probability is set to $\rho_p = 0.22$, implying that the expected number of pages viewed per query is $\mathbb{E}[p] = 1/(1-\rho_p) \approx 1.5$. In addition, a hierarchy filtering probability of $\rho_h = 0.22$ is used to simulate the likelihood that a user applies a category filter at each successive level. The click-through rate for products is $c = 0.024$, and conditional on a click, the purchase intent rate is $\pi_{\text{purchase}} = 0.014$.

Each simulation run consists of $T_{\max} = 600{,}000$ sequential user queries, with $s = 42$ products displayed per page. Key simulation metrics, such as the cumulative number of purchases, are recorded at regular intervals of 1,000 queries.

The core experimental variable is the product sorting strategy, controlled by the Boolean parameter $B_{\text{sorted}}$. In the control condition ($B_{\text{sorted}} = \text{False}$), products are presented using the fixed global sorting function, denoted $\text{SortGlobal}$. In contrast, the treatment condition ($B_{\text{sorted}} = \text{True}$) employs the hyper-personalized sorting function, denoted $\text{SortHyperPersonalized}$. This parameter set establishes the context within which the impact of the sorting strategy on cumulative purchases and other performance metrics is evaluated.

Results

The simulation was executed for 100 independent runs under each sorting condition, yielding a total of 200 simulation outputs. We aggregated these results to analyze the cumulative number of purchases, $P(t)$, over time and to examine differences between the fixed global sorting condition (FGS) and the hyper-personalized sorting condition (HPS).

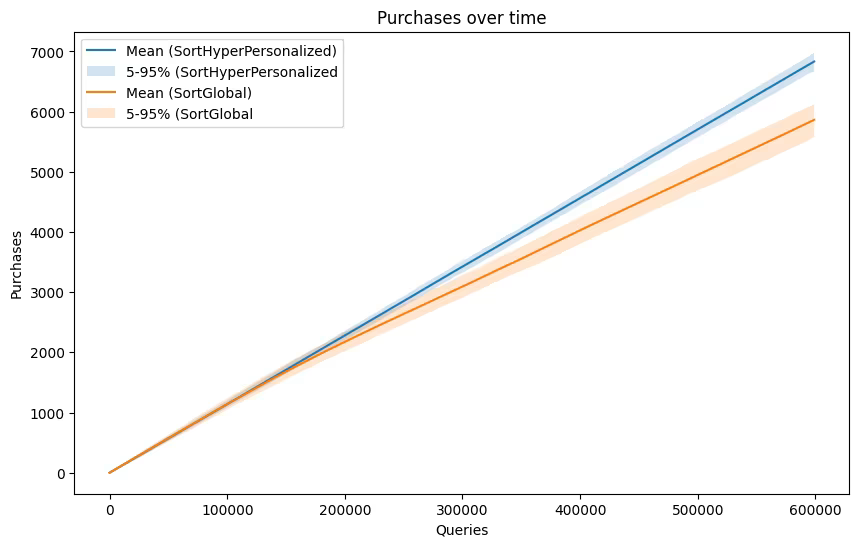
Figure 1 plots the mean cumulative purchases as a function of the number of user queries. The solid lines indicate the average trajectory across the 100 runs for each condition, while the shaded areas represent the 90% empirical confidence intervals (from the 5th to the 95th percentile) at each query point. As expected, cumulative purchases increase monotonically with the number of queries in both cases. However, a clear divergence emerges early: the mean trajectory for the hyper-personalized condition, $P_{\text{HPS}}(t)$, consistently lies above that for the fixed global sorting condition, $P_{\text{FGS}}(t)$. In other words, on average, more purchases occur when products are not presented in a fixed global order.

Furthermore, the 90% confidence intervals for the two conditions show minimal overlap beyond the first 10,000–20,000 queries. In many instances, the lower bound for the hyper-personalized condition closely approaches or even exceeds the upper bound for the fixed global sorting condition, suggesting that the difference in cumulative purchases is statistically significant.

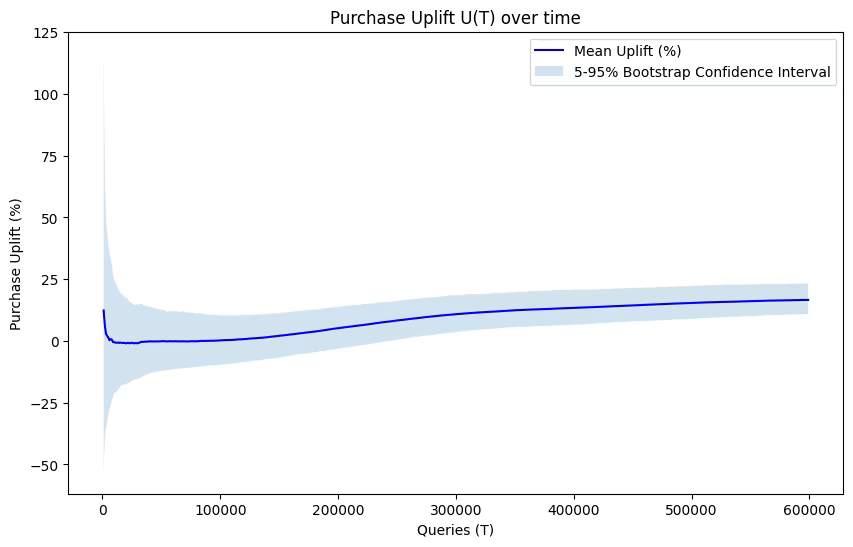
To formally assess and quantify the impact of the sorting strategy over time, we performed a bootstrap analysis. Figure 2 illustrates the mean percentage uplift in cumulative purchases, defined as

along with the 90% bootstrap confidence interval derived from 10,000 bootstrap samples. The uplift $U(t)$ is initially near zero but quickly becomes negative, reaching a maximum magnitude of approximately $-16.4\%$ around 500,000–600,000 queries.

Importantly, the 90% confidence interval for $U(t)$ remains entirely below zero after the first few thousand queries. According to our pre-defined decision criteria, this consistent exclusion of zero leads us to reject the null hypothesis at the $\alpha = 0.10$ significance level. These results provide strong evidence that the fixed global sorting strategy results in a statistically significant reduction in cumulative purchases compared to the hyper-personalized approach.

The dynamic nature of the uplift suggests that the negative impact of fixed global sorting is most pronounced during the early-to-middle stages of user interaction. This pattern is consistent with the hypothesis that a fixed sorting order accelerates the depletion of high-visibility items, thereby reducing the likelihood of subsequent purchases. As the simulation progresses and inventory constraints tighten, the relative disadvantage of fixed global sorting diminishes, although it remains statistically significant throughout the observed timeframe.

Conclusion

In this study, we used a hierarchical simulation model to examine how two product sorting strategies—Fixed Global Sorting versus Hyper-Personalized Sorting—affect cumulative purchase volume, denoted by $P(t)$, in a simulated e-commerce environment. Our model incorporated key elements of online retail, including multi-level product hierarchies, product variants with depletable stock, and probabilistic user behaviors related to browsing and purchasing.

Empirical findings from 100 simulation runs per condition reveal a clear and statistically significant divergence between the two strategies over 100,000 user queries. Specifically, the Fixed Global Sorting condition (with $B_{\text{sorted}} = \text{True}$), which yields cumulative purchases $P_{\text{FGS}}(t)$, consistently resulted in lower purchase volumes compared to the Hyper-Personalized Sorting condition (with $B_{\text{sorted}} = \text{False}$), which produces $P_{\text{HPS}}(t)$. A bootstrap analysis confirmed this difference: the relative uplift,

was statistically negative for the vast majority of the simulation period at an $\alpha=0.10$ significance level. The negative uplift was most pronounced early on—reaching roughly $-30\%$—and then gradually diminished, approaching about $-2\%$ by the end of the simulation.

These results challenge the notion that a fixed global sort order inherently improves sales performance. Although such sorting can enhance the visibility of top-ranked items through the primacy effect, it may also accelerate the depletion of popular product variants, resulting in missed opportunities later when key inventory is exhausted. In contrast, a Hyper-Personalized Sorting strategy, by more evenly distributing product visibility, appears to preserve inventory and ultimately drive higher cumulative purchases.

The implications for e-commerce practitioners are significant. Relying solely on fixed global sorting strategies may inadvertently restrict sales by prematurely depleting high-demand items. Our findings underscore the need for more dynamic, data-driven merchandising approaches that account for factors such as inventory levels, product diversity, and nuanced user preferences. Future work should extend this analysis by exploring different parameter settings and incorporating additional performance metrics, such as revenue or long-tail discovery, to provide a more comprehensive view of sorting strategy impacts.

In summary, this simulation study demonstrates that deliberate product ordering does not guarantee improved performance. Instead, a hyper-personalized approach may offer a more effective means of sustaining sales over time, highlighting the importance of adaptive merchandising strategies in the evolving landscape of online retail.